中学受験の応援サイト　中学受験ルネッサンス

基本的な線分図を、正確にかけるようにしよう！

これは、数や量を線の長さで表す　という考えです。
小３で学習した棒グラフが基本です。

この線分図を使う特殊算は、
植木算、和差算、年齢算、差集め算、倍数算などがあり
比の文章題でも必要となってきます。


まず、和差算の基本型.
これはわりとすぐ理解できます。

例題その１

お父さんの体重と僕の体重をあわせると１０４kgで
体重の差は４０kgです。それぞれ何kgですか？

では、線分図を書いてみましょう



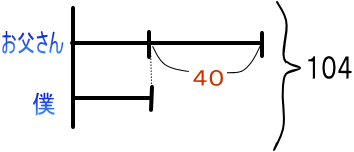
このように「なりますねえ。
あとは省略

例題その２

お兄ちゃんと僕は遊戯王カードを集めています。
お兄ちゃんの枚数は僕の2倍より4枚少なく
合わせて38枚です。
それぞれ何枚もっているか？

ここで「2倍より4枚少ない」という表現が
線分図として、すんなり書けない子がいます。

こうですねえ



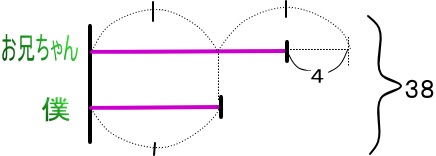
求め方は
３８＋４＝４２　で、山 ３つ分ができます。
３つ分が４２だから
４２÷３＝１４　で
僕は14枚となります。

この2倍になっている・・とか
3倍になっているなどの表現を
線分図として正確に書ける練習をまずしてください。


この基本が身についていると
比の文章題でもこわがることはありません

例題その３

お姉ちゃんとわたしは、「ＡＫＢ４８」のカードを集めています
お姉ちゃんとわたしの持っている枚数の比は、
７：5でその差は１２枚です
それぞれ何枚持っていますか？

線分図はこうなります




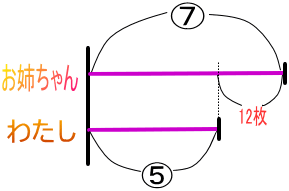
ここでは比の差を考えます。
�F−�D＝�Aですね
これが、12枚に当ります

だから、�A＝12枚　で
�@＝６枚です
わたしは、�D持っているから
６×５＝３０枚　
持っています。


枚数も、体重も、体積も、比の大きさも
すべて線分図で表せます。

是非、この考え方をマスターしてください。

---